Optimization for B+Trees

Optimization

这是真实的 DBMS中会使用到的东西，这能让我们的 B+Tree更快

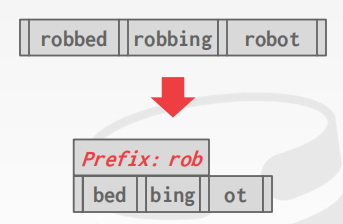
Prefix Compression

前缀压缩

前提：node中的 key是排好序的

实际上，保存在同一个 node上的 key彼此之间会非常相似

对于这种场景，我们可以将这些 key的公共前缀进行提取，那么剩下来的便是不相同的部分，即压缩了数据

对于聚簇索引，我们同样可以进行类似优化，我知道我所有的 tuple都存放在 磁盘或 page中，同样，在索引中也是排好序存在的，那么这些 tuple很有可能都在同一个节点上，它们的 record会指向相同的 page id，即它们最终都会落在同一个 page上，所以我们无需将单个 tuple的 page id重复进行存放，只需要保存一次 page id，然后将它们的 offset值和 slot分别存放

• 个人理解：record id -> page id + slot id

Suffix Truncation

后缀截断 --> 与前缀压缩相反的操作

其实这就是 "列前缀"

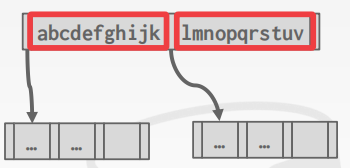
基本思路：我们无需在 inner node中保存完整的 key来当做 "路标"，我们可以在 inner node中来 存放能够区分 key的唯一前缀 即可，然后将剩余的后缀 drop

如果插入了某些数据，可能就会违反这个，那我们就得要对它进行维护，我们必须对此进行排序或者重新整理

但在实战中，如果数据没有发生太大改变的话，那么这种做法就可能非常棒

通常，使用前缀压缩会多于后缀截断！

Bulk Insert

基于大型数据集 进行索引的创建时的处理方案

在实战中，通常会遇到数据集的插入的方式，对于这种我们并不会一开始就去进行逐一加载，来构建我们的索引，因为这代价是在太高，因为这些 tuple的插入可能就会导致 "重构索引"

通常，我们会先将这些数据集加载到表中后，然后再回过头来添加索引 (这里实则就是 "首次索引的创建")，否则的话代价就会太高

即在插入数据时，不需要去试着维护索引，因为这样做代价太高了

可以使用 "从下往上构建索引"的方式，区别于之前的从上往下

• 首先先对拿到的 keys进行排序
• 然后将它们排列在叶子节点上，将它们正确填入到叶子节点中
• 然后从下往上走，只需要使用中间 key来填充 inner node，并且来生成我们的指针

索引创建完成之后，之后再进行的操作便和之前的处理方式一致了

Pointer Swizzling

搜索树时，在比对 Key之后，去别的节点进行搜索，会通过 "指针"从一个节点跳到下一个节点

实际上，我们所保存的 并不是原始的内存指针，而是 page id

我们会拿到 page id，然后会去 buffer pool那里，如果对于的 page不在内存中，那么 buffer pool会进行读取，然后返回一个指向此 page的指针，拿到对应的指针后，便可以进行下一步的搜索遍历了

叶子节点处，相邻叶子节点的访问，实际上保存的也是对应节点的 page id

即在运行过程中，会到 buffer pool管理这边，让它 将 page id转换为指针

实际上，这是很缓慢的操作，因为这个过程中，我们会去将 latch锁定 hashtable，以确保对应的 page不会被 drop，在这一系列复杂的操作后，page id才会被转换为 对应 page的指针

Pointer Swizzling的思路：如果我知道 固定在内存中的 page，这就意味着，我知道它们不需要从内存中移除出去，这时候就 不需要再去保存 page id，而是对应 page的指针，这就避免了去访问 buffer pool，也能够准确地拿到我想要的数据

需要确保的是，当对应的 page从内存中移除，也就是将它写到磁盘上(这里也可以是被 drop 掉)，此时不会去保存 page指针 (当 page再被读进内存时，对应的是不同的内存地址)

实际上，我们也无需将 page id删除，可以通过一点额外的元数据来表示，这里是我们想要的指针，而不是 page id

通常我们可以将所有的上层节点保留下来，因为这些节点是高频率节点 (搜索叶子节点时，必须经过上层节点)